Guía práctica para la habilidad matemática de Representar: dificultades, estrategias y actividades efectivas

¿Has notado que algunos estudiantes pueden resolver un problema con números, pero se confunden cuando deben usar diagramas o tablas? Esto puede estar relacionado con una habilidad fundamental en el aprendizaje matemático: la habilidad de representar. En este artículo te explicaremos qué significa representar en matemáticas, por qué es clave para desarrollar el pensamiento matemático, cuáles son los errores más frecuentes de los estudiantes y cómo enseñarla de manera efectiva en el aula.

¿Qué significa representar en matemáticas y por qué es importante?

Representar es una de las competencias matemáticas definidas por el Ministerio de Educación de Chile (MINEDUC, 2012) y por organismos internacionales como la OCDE (PISA, 2022) y el NCTM (2000). Esta habilidad consiste en usar diversos tipos de lenguaje o formas de expresión para conseguir comunicar información, ideas, relaciones o procesos matemáticos. Esto puede incluir:

• Diagramas, tablas y gráficos.
• Lenguaje algebraico, simbólico o verbal.
• Representaciones concretas (material).
• Modelos geométricos o pictóricos.

Un ejemplo concreto es el siguiente:

“Observa las siguientes imágenes y responde la pregunta:

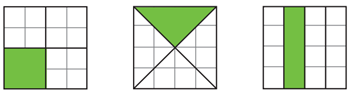
¿Es correcto afirmar que, al representar una fracción, la figura inicial se debe dividir en partes de igual forma e igual tamaño? Justifica tu respuesta”.

Así, como plantea Duval (2006), representar corresponde a transformar un problema de una forma a otra para hacerlo comprensible. Por ejemplo, transformar un texto a un gráfico, o un dibujo a una expresión algebraica. Esta conversión es clave para acceder al significado matemático. Además, Goldin (2002) destaca que los estudiantes con habilidades sólidas de representación pueden explorar problemas con mayor nivel de profundidad y construir mejores estrategias de resolución para ellos.

Estrategias prácticas para desarrollar la habilidad de representar, según nivel

1. Nivel Inicial y Primer Ciclo Básico:

• Usar material concreto, como bloques y figuras, para representar cantidades y operaciones.
• Pedir a los estudiantes que dibujen lo que ocurre en un problema matemático.
• Incorporar pictogramas y gráficos simples para representar datos de encuestas.
• Relacionar las representaciones con experiencias cotidianas.

2. Segundo Ciclo Básico:

• Relacionar tablas con gráficos de barras y de líneas, analizando patrones.
• Usar esquemas o diagramas de flujo para representar procesos como algoritmos.
• Comparar diferentes formas de representar la misma información y discutir ventajas de cada una.
• Incorporar contextos reales como deportes, clima o economía familiar para representar datos.

3. Nivel Medio:

• Modelar situaciones reales con funciones y expresiones algebraicas.
• Representar variaciones con gráficos cartesianos y analizar sus propiedades.
• Fomentar la creación de modelos propios (por ejemplo, representaciones de datos en Excel o GeoGebra).
• Promover la vinculación entre representaciones simbólicas y gráficas en problemas de geometría y estadística.

Principales dificultades en la adquisición de la habilidad de representar

Muchos estudiantes presentan dificultades al:

• Usar un solo tipo de representación y no conectar con otras, por ejemplo, representando datos con una tabla pero no relacionándolos con un gráfico de barras.
• Elegir representaciones que no son pertinentes al problema, por ejemplo, usando un gráfico circular para comparar evoluciones temporales.
• No interpretar correctamente recursos como gráficos o diagramas, por ejemplo, interpretando mal un diagrama de fracciones creyendo que 1/3 es mayor que 1/2.
• Memorizar procedimientos sin comprender el significado, por ejemplo, trazando siempre una recta en planos cartesianos sin entender la relación entre variables.

Estas dificultades suelen estar ligadas a una enseñanza centrada solo en lo simbólico, sin transitar entre distintos registros de representación (Duval, 2006), o sin dar espacios a los estudiantes para crear sus propias representaciones. También puede influir una falta de modelamiento de parte del docente, donde no se explicita el propósito ni el valor de las representaciones utilizadas en la clase.

Errores frecuentes que debemos identificar y abordar

1. Confundir el tipo de gráfico o tabla a utilizar. Por ejemplo, usar un gráfico circular para datos que varían en el tiempo.
2. Representar de manera superficial, sin conectar con el significado del problema. Dibujar sin pensar en lo que se quiere comunicar.
3. No traducir adecuadamente de un registro a otro (por ejemplo, de texto a diagrama). Esto puede producir errores de interpretación o solución.
4. Uso mecánico de representaciones sin fines comunicativos o explicativos. Como hacer un gráfico “porque lo pide el libro”, sin entender su utilidad.
5. Errores de escala y proporcionalidad. Por ejemplo, construir un gráfico de barras donde las alturas no corresponden con los valores representados.
6. Falta de rotulación y claridad en los elementos. Un gráfico sin título, sin ejes nombrados o sin unidades se vuelve difícil de interpretar.
7. Creencia de que solo lo simbólico es “matemático”. Algunos estudiantes no valoran sus esquemas o dibujos como herramientas válidas para pensar matemáticamente.

Detectar estos errores implica observar con atención el proceso de resolución de los estudiantes, más allá del producto final. Muchas veces un error en la representación refleja una comprensión parcial o incorrecta del problema, por lo que debe ser abordado desde el análisis conceptual y no solo como un fallo de tipo gráfico.

Cómo enfrentar los errores comunes en la representación

• Proponer tareas abiertas, donde los estudiantes deben elegir y justificar su representación.
• Comparar representaciones de distintos estudiantes y promover la metacognición: ¿por qué elegiste esa forma?, ¿funciona para todos?, ¿qué representa cada parte?
• Enseñar a traducir entre registros: verbal, pictórico, simbólico, tabular, gráfico.
• Utilizar errores frecuentes como base para el análisis colectivo.
• Diseñar instancias de autoevaluación donde el estudiante revise si su representación es clara, precisa y útil.
• Utilizar el andamiaje progresivo, comenzando con representaciones concretas y guiadas para luego avanzar hacia formas más abstractas.
• Implementar sesiones de resolución colaborativa, donde los estudiantes dialoguen y corrijan colectivamente sus representaciones.
• Incorporar actividades de “reparación de errores”, donde se presenten representaciones incorrectas y los estudiantes deban corregirlas y justificar los cambios realizados.
• Promover el uso de herramientas digitales que permiten visualizar, manipular y corregir representaciones (GeoGebra, Desmos, Excel, entre otros), lo cual también ayuda a interiorizar conceptos dinámicamente.

Vinculación con el currículum y evaluación de la habilidad

En las Bases Curriculares de Matemática (MINEDUC, 2012), la habilidad de representar aparece transversalmente en todos los niveles y ejes, lo que implica que debe ser abordada en geometría, álgebra o estadística. Evaluar esta habilidad requiere considerar tanto la variedad de representaciones utilizadas como su pertinencia y aporte a la resolución del problema.

Por ejemplo, al evaluar un gráfico, no basta con verificar si está completo, también se debe determinar si ayuda a interpretar los datos y responder a la pregunta planteada. En este sentido, las rúbricas y listas de cotejo pueden ser herramientas útiles para retroalimentar el proceso.

Reflexiones finales

Finalizando, podemos establecer que la habilidad de representar permite a los estudiantes hacer visible su pensamiento matemático. No se trata de adornar una solución con un gráfico, es desarrollar la comprensión profunda de las relaciones matemáticas. Por eso, representación y comprensión van de la mano.

Como docentes, fomentar esta habilidad implica dar espacio para explorar, traducir, comparar y justificar diferentes formas de expresar el pensamiento. Enseñar con un enfoque en la representación enriquece la clase, incluye a más estudiantes y fortalece notablemente el aprendizaje.

Además, es clave recordar que representar también implica dialogar: cuando un estudiante explica con sus palabras, esquemas o gráficos lo que entiende, está construyendo sentido. Por ello, representaciones y comunicación matemática deben ir de la mano para transformar la sala de clases en un espacio de aprendizaje activo y significativo.

-

¿Te pareció interesante esta publicación? ¡Compártela con otros docentes! Recuerda que en Umáximo encontrarás variados recursos asociados a las habilidades matemáticas. Si aún no tienes una cuenta en Umáximo, crea la tuya aquí y accede a recursos exclusivos diseñados para profesores.

Referencias

• Ministerio de Educación de Chile (MINEDUC). (2012). Bases Curriculares 1º a 6º básico. Santiago: MINEDUC.
• OECD. (2022). PISA 2022 Mathematics Framework.
• NCTM (2000). Principles and Standards for School Mathematics.
• Duval, R. (2006). "Aprender matemáticas: del registro de representación al significado". Revista Suma.
• Goldin, G. (2002). Representations in mathematical learning and problem solving.
• Ministerio de Educación de Chile (2020). Unidad de Currículum y Evaluación. Marco para la Buena Enseñanza. Referente para la docencia en matemática.